Il faut savoir que les codes cycliques sont en fait une amélioration
des codes polynomiaux (que je n'ai pas traité ici) qui sont eux
même des codes linéaires systématiques.
Définition :
Un code linéaire est dit cyclique s’il est stable par permutation
à droite, c’est à dire : 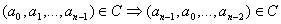 .
L’algèbre
.
L’algèbre 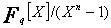 est un espace vectoriel de dimension
est un espace vectoriel de dimension  dont
dont 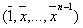 est une base
- démonstration.
On peut alors identifier le vecteur
est une base
- démonstration.
On peut alors identifier le vecteur 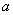 de
de 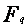 au polynôme
au polynôme
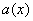 .
.
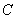 est un sev de
est un sev de 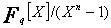 ,
comme il est cyclique on a
,
comme il est cyclique on a 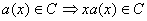 .
.
Donc par récurrence, pour tout polynôme 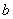 on a
on a 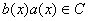 d’où
d’où
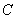 est un idéal de
est un idéal de
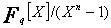 .
.
Car réciproquement, tout idéal de 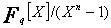 est un sous espace vectoriel stable par permutation à droite.
est un sous espace vectoriel stable par permutation à droite.
Comme cet anneau est principal, on a que 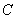 est engendré par
est engendré par 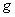 ,
où
,
où 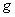 est un polynôme
de
est un polynôme
de  qui divise
qui divise 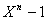 ,
de plus
,
de plus 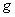 est unique lorsqu’on
le choisi unitaire - démonstration.
est unique lorsqu’on
le choisi unitaire - démonstration.
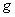 s’appelle le polynôme
générateur de
s’appelle le polynôme
générateur de 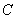 .
.
Donc un code cyclique est un code polynomial dont le polynôme générateur
divise 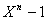 .
.
Principe de codage:
On obtient le mot codé 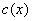 associé au mot initial
associé au mot initial 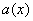 de cette façon
de cette façon 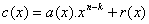 où
où 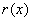 est le reste
de la division euclidienne de
est le reste
de la division euclidienne de 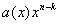 par le polynôme générateur
par le polynôme générateur  que l’on note ainsi
que l’on note ainsi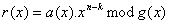 .
Donc
.
Donc 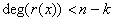 .
.
On remarque que les 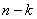 bits de
bits de 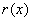 forment les
bits du champ de contrôle, de plus les bits de poids fort forment
le mot initial, c’est un code systématique.
forment les
bits du champ de contrôle, de plus les bits de poids fort forment
le mot initial, c’est un code systématique.
Principe de détection des erreurs :
A la réception, chaque mot reçu 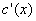 est divisé par le polynôme générateur
est divisé par le polynôme générateur  et un reste non nul indique qu'il y a eu erreur lors de la transmission.
et un reste non nul indique qu'il y a eu erreur lors de la transmission.
Recherche des polynômes générateurs :
On considère le corps algébriquement clos de 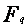 .
Dans un tel corps on a :
.
Dans un tel corps on a :  où
où 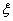 est une racine
n.ième primitive de l’unité dans
est une racine
n.ième primitive de l’unité dans 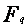 .
.
On peut considérer que le corps 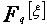 est un espace vectoriel de dimension
est un espace vectoriel de dimension  sur
sur 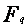 . On considère
alors l’ensemble
. On considère
alors l’ensemble  .
On a donc que
.
On a donc que 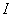 est un idéal de
est un idéal de  d’où
d’où 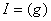 .
Comme
.
Comme 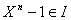 , on a
alors
, on a
alors 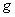 qui divise
qui divise 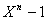 .
On en déduit que
.
On en déduit que 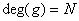 (théorème du cours de MP).
(théorème du cours de MP).
D’après Galois : (résultat admis)
On a 
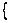 automorphisme
de corps de
automorphisme
de corps de 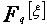 qui
laisse
qui
laisse 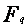 invariant
invariant 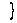 .
.
D’où 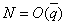 dans
dans 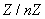 (où
(où
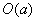 représente
l’ordre de l’élément
représente
l’ordre de l’élément 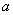 ).
).
On recherche alors les polynômes de  de degré
de degré  qui divisent
qui divisent 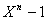 .On
s’intéressera aux polynômes unitaires.
.On
s’intéressera aux polynômes unitaires.
Soit 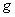 un diviseur de
un diviseur de
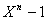 dans
dans  ;
;  : où
: où  est une partie de
est une partie de 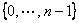 .
On identifie alors l’ensemble
.
On identifie alors l’ensemble 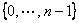 à
à 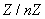 .
.
Proposition :
Soit  une partie
de
une partie
de 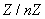 .
. 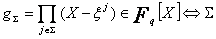 est stable par permutation par
est stable par permutation par 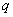 : démonstration.
: démonstration.
Il suffit alors de trouver une partie  de
de 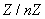 de
de  éléments stable par permutation par
éléments stable par permutation par 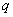 ,
on pourra alors construire un polynôme générateur.
Exemple de construction
d'un polynôme générateur.
,
on pourra alors construire un polynôme générateur.
Exemple de construction
d'un polynôme générateur.