Notes préliminaires :
Dans toute la suite, on notera 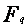 un corps fini de
un corps fini de 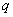 éléments
; on a donc
éléments
; on a donc 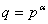 où
où 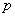 est premier
: démonstration.
est premier
: démonstration.
Matrice de contrôle et matrice génératrice :
Un code linéaire de dimension 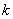 et de longueur
et de longueur  est un
sous espace vectoriel de
est un
sous espace vectoriel de 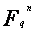 (si
(si 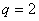 c’est
alors un code binaire).
c’est
alors un code binaire).
Toute matrice 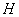 du type
du type 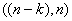 vérifiant
vérifiant
 est appelé
matrice de contrôle de
est appelé
matrice de contrôle de 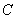 .
On a
.
On a 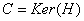 et
et 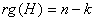 .
.
Si on note 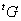 la
matrice de l’application linéaire
la
matrice de l’application linéaire 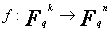 ,
on a alors
,
on a alors 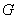 du
type
du
type 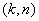 qui est la matrice
génératrice du code ;
qui est la matrice
génératrice du code ; 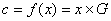 .
.
Le code systématique :
Le code systématique consiste en la concaténation du mot
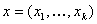 avec
avec 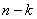 symboles
symboles 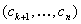 dépendants
linéairements des
dépendants
linéairements des 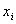 .
Les
.
Les 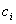 sont les bits
de contrôles. On a alors un mot du code du type :
sont les bits
de contrôles. On a alors un mot du code du type : 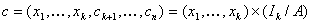 où
où
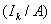 désigne la
matrice de taille
désigne la
matrice de taille 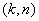 obtenue en écrivant cote à cote la matrice identité
de taille
obtenue en écrivant cote à cote la matrice identité
de taille 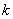 et une matrice
et une matrice
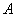 quelconque.
quelconque.
On dit d’un code qu’il est systématique s’il
existe une matrice génératrice du type 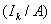 .
Dans ce cas on a
.
Dans ce cas on a 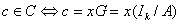 et on a également
et on a également 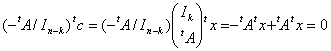
D’où 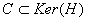 où
où 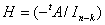 . Comme
. Comme
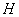 est de rang
est de rang 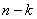 ,
les sev
,
les sev 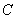 et
et 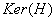 ont même dimension
ont même dimension 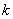 et donc
et donc 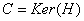 . La
matrice
. La
matrice 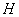 est par
conséquent une matrice de contrôle de
est par
conséquent une matrice de contrôle de 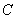 .
.
Par conséquent, en ce qui concerne les exemples, le
code de parité est donc un code systématique  ,
le code à répétition
un
,
le code à répétition
un 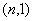 .
.