On notera dans toute la suite 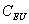et 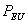respectivement la valeur du Call et celle du Put européen. De même, on notera 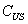et 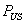les valeurs du Call et du Put américain.

La méthode de Monte-Carlo :

Soit 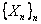une suite de variables aléatoires indépendantes identiquement distribuées, alors .
La valeur d’un Call étant de 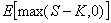, la méthode de Monte-Carlo semble être une technique efficace pour calculer le prix d’une option. Il suffira en effet de simuler un grand nombre de fois 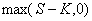et d’en prendre la moyenne. Pour ce faire il faudra déterminer la valeur du sous-jacent.

Détermination de la loi du sous-jacent :

On considéra dans toute la suite un sous-jacent de valeur 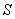qui vérifie :

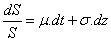
En posant 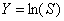, on obtient grâce à la formule d’Îto :

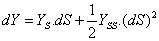
D’où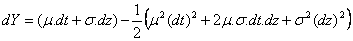
Puis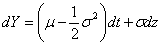
Enfin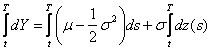
On pose alors 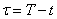et on obtient :

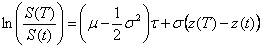
D’où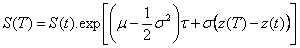

On obtient alors une fonction qui nous permet de déterminer la valeur du sous-jacent à tout instant. Ceci va être très important pour la suite de l'étude car si le model binomial et le model de Black et Sholes peuvent s’appliquer sans connaître la loi du sous-jacent (ceci est tout de même nécessaire si on veut démontrer la formule de Black et Sholes et la technique du model binomial) la technique de Monte-Carlo nécessite de simuler le sous-jacent (et donc il faut connaître sa loi).

Théorème de Girsanov :

Soit un espace probabilisé filtré, un brownien standard et 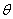un processus borné adapté à valeurs réelles.
On définit un processus 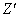et une mesure 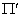en posant :
et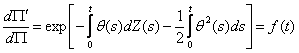
avec 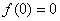et .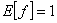
Alors 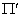est une mesure de probabilité et 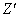un brownien standard sous 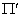. Avec 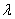une constante, la densité de 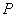par rapport à est définie su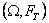r par :


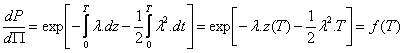
Soit 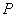la probabilité définie par :


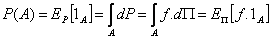
Alors 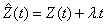est un brownien. Comme on a 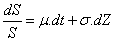sous et avec 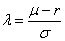on obtient :
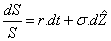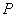sous qui est la probabilité risque neutre.
D’où : (*)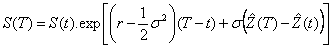

D’une manière générale, on se placera en univers risque neutre.