Dans la mesure où l’évaluation du cours de l’option
repose exclusivement sur la simulation du cours du sous-jacent, et comme
celui-ci est fortement impacté par le versement du dividende, la
valeur de l’option va donc subir cet événement. La
technique de simulation de la valeur du sous-jacent doit donc être
modifiée pour tenir compte de l’influence engendrée
par le versement du dividende. Le principe général reste
identique, seul l’implémentation de l’évaluation
de 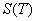 va être modifiée.
va être modifiée.
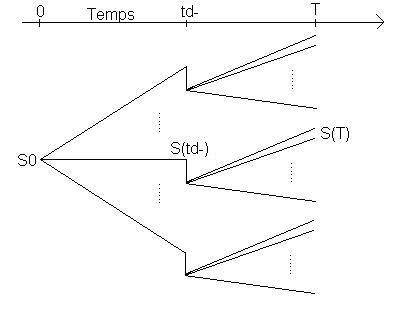
La technique de simulation reste la même jusqu’à la
date de versement du dividende. On simule un grand nombre de fois 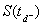 qui est la valeur du sous-jacent juste avant le versement du dividende.
On obtient alors le valeur
qui est la valeur du sous-jacent juste avant le versement du dividende.
On obtient alors le valeur 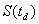 en retranchant la valeur du dividende à la valeur
en retranchant la valeur du dividende à la valeur 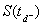 .
Pour chaque valeur de
.
Pour chaque valeur de 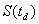 on simule un grand nombre de fois la valeur de
on simule un grand nombre de fois la valeur de 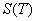 .
On obtient une valeur du Call pour chaque valeur de
.
On obtient une valeur du Call pour chaque valeur de 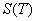 ; on obtient finalement la valeur du Call théorique en effectuant
la moyenne de toutes les valeurs des Call obtenus.
; on obtient finalement la valeur du Call théorique en effectuant
la moyenne de toutes les valeurs des Call obtenus.
Vérifions à présent si cette technique intuitive
est valable. On ne peut plus comparer notre résultat avec celui
obtenu par la formule de Black & Scholes, en effet cette formule n’est
plus utilisable car le versement du dividende scinde notre option en deux
parties distinctes. Il convient alors d’utiliser un modèle
discret : le modèle binomial.
Supposons que le marché offre un rendement sans risque 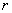 et un actif risqué, que nous symboliserons par une action de prix
et un actif risqué, que nous symboliserons par une action de prix
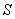 en 0 qui procure
en 0 qui procure 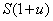 en 1 si le marché est à la hausse et
en 1 si le marché est à la hausse et 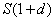 si le marché est à la baisse. On a
si le marché est à la baisse. On a 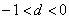 et
et 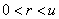 , par ailleurs
on note
, par ailleurs
on note 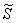 la valeur
à priori de l’actif en 1.
la valeur
à priori de l’actif en 1.
Comme on dispose de 2 actifs primaires et que l’univers possède
2 états de la nature ; le marché est donc complet. On notera
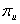 et
et 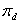 respectivement les probabilités risque neutre de hausse et de baisse
du marché. Considérons à présent un Call
respectivement les probabilités risque neutre de hausse et de baisse
du marché. Considérons à présent un Call 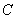 sur cette action de prix d’exercice
sur cette action de prix d’exercice 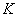 .
Pour obtenir la valeur de l’option à l’équilibre,
nous allons procéder par duplication…
.
Pour obtenir la valeur de l’option à l’équilibre,
nous allons procéder par duplication…
Il est clair que la valeur de l’option en date 1 est 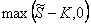 .
Définissons
.
Définissons 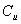 et
et 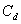 par :
par :
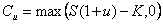 et
et 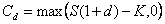
Le portefeuille de duplication de l’option est obtenu en investissant
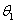 dans l’actif
sans risque que l’on suppose de prix 1 en 0, et
dans l’actif
sans risque que l’on suppose de prix 1 en 0, et 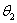 dans l’actif risqué. Ce portefeuille est donc défini
par :
dans l’actif risqué. Ce portefeuille est donc défini
par :
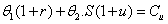 et
et 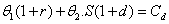
D’où 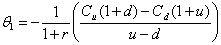 et
et 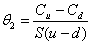
Comme on a 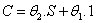 on en
déduit :
on en
déduit :
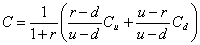
Il faut, dans un premier temps, simuler l’arbre de 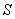 .
Pour cela, on applique la technique précédente 49 fois.
On obtient un arbre de 50 branches ; plus le nombre de « pas »
–le nombre de fois que l’on applique la technique– est
important plus la valeur obtenue est fine. Si le nombre de pas tend vers
l’infini, l’intervalle entre chaque pas diminue et on passe
alors d’un processus discret à un processus continu. En effet,
la valeur du modèle binomial converge vers celle donnée
par la formule de Black & Scholes lorsque celle-ci est applicable,
c'est-à-dire en l’absence de dividende.
.
Pour cela, on applique la technique précédente 49 fois.
On obtient un arbre de 50 branches ; plus le nombre de « pas »
–le nombre de fois que l’on applique la technique– est
important plus la valeur obtenue est fine. Si le nombre de pas tend vers
l’infini, l’intervalle entre chaque pas diminue et on passe
alors d’un processus discret à un processus continu. En effet,
la valeur du modèle binomial converge vers celle donnée
par la formule de Black & Scholes lorsque celle-ci est applicable,
c'est-à-dire en l’absence de dividende.
Dans l’univers réel, on a : 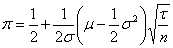
Dans l’univers risque neutre, on a : 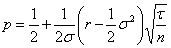
En posant 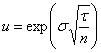 et
et 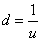 ,
on obtient
,
on obtient 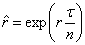
D’où 
Quand 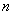 devient grand,
et en utilisant le développement limité de l’exponentiel,
on obtient :
devient grand,
et en utilisant le développement limité de l’exponentiel,
on obtient :
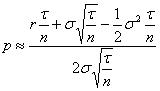
D’où, dans l’univers risque neutre, il vient :
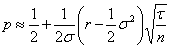
Par ailleurs, dans cet univers risque neutre, en notant 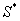 le cours en
le cours en  dans le
processus binomial, on obtient :
dans le
processus binomial, on obtient :
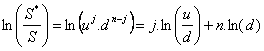
où 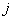 suis une loi
binomiale de paramètres
suis une loi
binomiale de paramètres 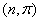 dans l’univers réel, et
dans l’univers réel, et 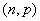 dans l’univers risque neutre. On a :
dans l’univers risque neutre. On a :
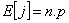 et
et 
D’où 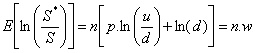 et
et 
Or 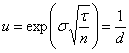 ce qui implique
que
ce qui implique
que 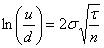 et on a alors
:
et on a alors
:
????????????????????????????????????????????????????
Et on obtient finalement :
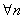
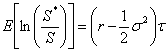
Donc l’égalité des espérances dans l’univers
risque neutre.
D’un autre côté, on a :

D’où 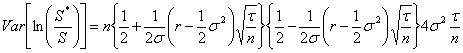
Et on obtient finalement :
Quand 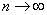
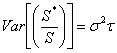
Notons à présent 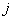 le nombre de hausses durant
le nombre de hausses durant 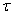 et
et 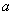 le nombre minimum
de hausses pour qu’il y ait exercice de l’option. On note
également
le nombre minimum
de hausses pour qu’il y ait exercice de l’option. On note
également 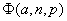 la probabilité que
la probabilité que 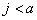 .
On déduit des résultats précédents que :
.
On déduit des résultats précédents que :
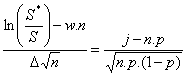
Thérorème de Lindenberg :
Comme 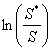 est une somme de
est une somme de 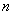 variables
aléatoires indépendantes équi-distribuées
suivant une loi binomiale de paramètres
variables
aléatoires indépendantes équi-distribuées
suivant une loi binomiale de paramètres 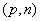 .
On a que
.
On a que 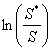 converge en loi vers celle
converge en loi vers celle 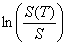 de c'est-à-dire vers la loi
de c'est-à-dire vers la loi 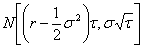 .
D’où on obtient que :
.
D’où on obtient que :
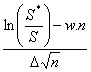 converge en loi
vers une loi normale centrée réduite
converge en loi
vers une loi normale centrée réduite 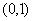 .
.
On en déduit également que 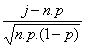 converge vers une loi normale centrée réduite
converge vers une loi normale centrée réduite 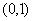 .
Revenons au calcul de :
.
Revenons au calcul de :
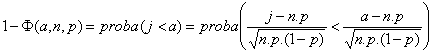
D’où 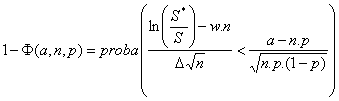
Or, pour que 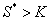 ,
il faut que
,
il faut que 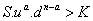 ,
d’où on obtient :
,
d’où on obtient :
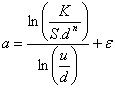 avec
avec 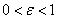 .
.
De même, il vient :
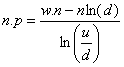 et
et 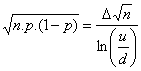
On en déduit finalement que :
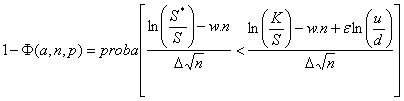
Quand 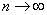 et
et  ,
on a alors :
,
on a alors :
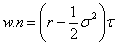
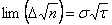
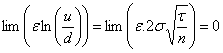
D’où on obtient :

Et 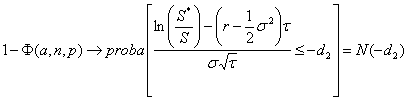
D’où il vient finalement :
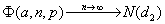
Le modèle binomial converge donc vers le modèle de Black
& Scholes. Il faudra donc tenir compte de cette convergence lors de
la comparaison entre les résultats de la simulation par Monte-Carlo
et les résultats du modèle binomial. En effet, l’écart
pourra être plus important que celui qui apparaîtra lorsque
l’on comparera Monte-Carlo avec Black & Scholes.
Simulation du modèle binomial :
Au bout des 49 pas on arrive à l’instant de versement du
dividende. On obtient 50 valeurs à partir desquelles on va créer,
pour chaque valeur obtenue, un arbre de 50 pas. On obtient donc valeurs
pour  .
.
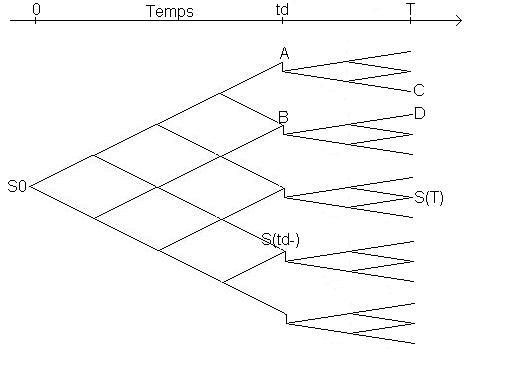
On remarque que l’on obtient en fait 50 blocs de 51 branches qui se présentent comme 50 arbres classiques. On peut noter que les valeurs de C et D sont distinctes, et que comparativement au valeurs de A et B pour lesquelles il est aisé de passer de l’une à l’autre, il n’existe pas de formule simple qui permette de passer de C à D.
A présent, il s’agit de remonter les valeurs de l’arbre
afin de déterminer la valeur actuelle du Call. Pour chaque valeur
de 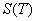 on regarde si on
a intérêt à exercer notre option : c'est-à-dire
si
on regarde si on
a intérêt à exercer notre option : c'est-à-dire
si 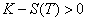 . Si
on exerce l’option, il faut alors remplacer
. Si
on exerce l’option, il faut alors remplacer 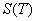 par
par 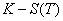 qui représente
le gain en
qui représente
le gain en  de l’exercice
de l’option. Sinon exercer l’option serait une perte car le
prix d’exercice est supérieur au prix du sous-jacent. On
remplace alors la valeur de
de l’exercice
de l’option. Sinon exercer l’option serait une perte car le
prix d’exercice est supérieur au prix du sous-jacent. On
remplace alors la valeur de 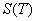 par 0 qui est la valeur du Call dans ces conditions. On peut alors remonter
chacun des 50 blocs par la méthode décrite précédemment
jusqu’à la date de versement du dividende. On aura effectué
50 remontés pour chacun des sous arbres. A présent on se
retrouve dans le cadre d’un seul arbre avec 50 valeurs qui sont
celles que l’on vient d’obtenir ; en remontant ce dernier
arbre on obtient la valeur théorique du Call en présence
d’un versement de dividende.
par 0 qui est la valeur du Call dans ces conditions. On peut alors remonter
chacun des 50 blocs par la méthode décrite précédemment
jusqu’à la date de versement du dividende. On aura effectué
50 remontés pour chacun des sous arbres. A présent on se
retrouve dans le cadre d’un seul arbre avec 50 valeurs qui sont
celles que l’on vient d’obtenir ; en remontant ce dernier
arbre on obtient la valeur théorique du Call en présence
d’un versement de dividende.
La différence entre les deux résultats peut être
réduite d’avantage en augmentant le nombre de simulation
dans la méthode de Monte-Carlo, ou en augmentant le nombre de pas
dans le modèle binomial.
La méthode de Monte-Carlo est efficace pour simuler la valeur d’un
Call européen en présence de dividende puisqu’elle
se rapproche des résultats obtenus par le modèle standard,
ici le modèle binomial. En cas de plusieurs dividendes, on applique
le même principe : a chaque date de versement de dividende, il y
a séparation des arbres, ce qui entraîne assez rapidement
d’importants calculs.
Dans le cas du Put, le principe est exactement le même, une fois
l’arbre construit, on regarde si l’exercice de l’option
est avantageux auquel cas on remplace la valeur de 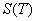 par
par 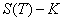 . Si on n’exerce
pas l’option, on remplace la valeur de
. Si on n’exerce
pas l’option, on remplace la valeur de 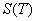 par 0. Enfin, on remonte l’arbre comme précédemment
afin d’obtenir la valeur théorique du Put.
par 0. Enfin, on remonte l’arbre comme précédemment
afin d’obtenir la valeur théorique du Put.
Conclusion :
La technique de Monte-Carlo est satisfaisante pour déterminer la valeur d’une option européenne, elle est dans son principe plus simple que Black & Scholes ou le modèle binomial mais son application est nettement plus lourde car elle nécessite de simuler un grand nombre de fois des variables gaussiennes, cela demande des outils informatiques performants. A l’inverse le modèle de Black & Scholes est théoriquement plus complexe, mais plus facilement réalisable ainsi que le modèle binomial qui peut être réalisé entièrement sans machine.
En ce qui concerne la qualité des résultats, la technique de Monte-Carlo est acceptable.