Introduction.

Une option portant sur une action est une possibilité d'achat ou de vente d'une action à un prix déterminé à l'avance, appelé prix d’exercice. Une option d'achat s'appelle un « Call » et une option de vente un « Put ». Il faut distinguer deux grandes catégories d'options : les options ne pouvant être exercées qu'à échéance –les options européennes– et celles que l'on peut exercer à tout moment –les options américaines.
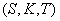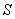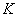Une option est définie par le triplet où représente la valeur du sous-jacent –la valeur de l’action–, représente le prix d’exercice et la maturité –la durée de vie de l’option.
Le seul paramètre inconnu est la valeur du sous-jacent, donc la détermination du prix d’une option dépend de cette valeur, les autres paramètres étant fixés à l’origine.
Le but de cette étude est de calculer cette valeur afin de déterminer les cours d'options sur actions. Pour calculer cette valeur il semble naturel d'utiliser la méthode de Monte-Carlo, celle-ci s'appuie principalement sur la loi des grands nombres.
Nous étudierons en premier lieu l’évaluation d’un Call et d’un Put européen sans versement de dividende, puis avec versement de dividende. Dans une deuxième partie nous évaluerons un Call américain avec versement de dividende puis en dernière partie, un Put américain sans versement de dividende.