Présentation générale et exercice de l'option :
Une option américaine se distingue de son homologue européenne
par la possibilité de l’exercer à tout instant. A
priori, pour son évaluation on doit donc s’intéresser
à cette possibilité, il faut alors calculer la valeur du
Call et donc celle de  à tout instant
à tout instant 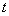 .
En effet, le détenteur d’une option décidera à
l’instant
.
En effet, le détenteur d’une option décidera à
l’instant 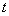 d’exercer son option si
d’exercer son option si 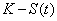 est
supérieur au prix d’un Call américain sur le même
sous-jacent valant
est
supérieur au prix d’un Call américain sur le même
sous-jacent valant  ,
de prix d’exercice
,
de prix d’exercice 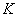 et de maturité
et de maturité ![]() .
.
On exerce l’option 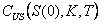 en
en 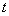 si
si  .
.
En effet, si 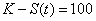 et si
et si  , alors
j’exerce mon option, je la rachète immédiatement,
on se retrouve dans la situation initiale mais enrichi de 10 qui représente
un gain certain.
, alors
j’exerce mon option, je la rachète immédiatement,
on se retrouve dans la situation initiale mais enrichi de 10 qui représente
un gain certain.
On remarque par cet exemple l’importance de la possibilité
d’exercice anticipé. Or il semble impossible de calculer
 de manière
continue.
de manière
continue.
Remarque sur l'exercice anticipée des options américaines :
En l’absence de dividende, une option américaine est une
option européenne avec le droit supplémentaire d’exercice
anticipé. A une date 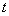 quelconque, on a donc logiquement :
quelconque, on a donc logiquement :
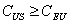
Or on sait que 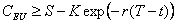 et que la valeur actuelle du prix d’exercice
et que la valeur actuelle du prix d’exercice 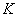 ,
à la date
,
à la date 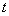 ,
est inférieur à
,
est inférieur à 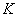 :
: 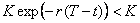 .
.
On peut donc écrire que 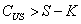 .
.
Cela signifie donc que la valeur du Call américain, en une date
quelconque 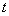 précédent
l’échéance et en l’absence de dividende, est
supérieure si l’option est conservée que si elle est
exercée.
précédent
l’échéance et en l’absence de dividende, est
supérieure si l’option est conservée que si elle est
exercée.
En présence de dividende, il peut être intéressant
d’exercer l’option juste avant le versement du dividende si
celui-ci est élevé afin de l’encaisser. Par contre
il n’est toujours pas intéressant de l’exercer à
une date quelconque. Ceci est démontré et l’ouvrage
de Hull « Options, Futures and Other Derivatives
» qui représente une référence en la matière.
Compte tenu de l’étude précédente, on a intérêt
à exercer l’option américaine uniquement à
l’échéance ou juste avant le versement d’un
dividende. Cela va simplifier considérablement le problème
initial du calcul de  ,
il suffit à présent de le calculer à quelques dates.
,
il suffit à présent de le calculer à quelques dates.
La technique d’évaluation de la valeur du Call américain
en présence d’un versement de dividende est donc exactement
la même que celle d’un Call européen en présence
d’un dividende, à la différence que l’exercice
du Call américain demeure possible à la date 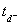 précédent le versement du dividende.
précédent le versement du dividende.
Simulation d'un Call américain en présence de dividendes avec la méthode de Monte-Carlo :
Dans un premier temps on simule un grand nombre de fois
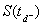 , il faut alors
regarder s’il y a exercice anticipé. Pour ce faire, on calcul
à l’aide de Black & Scholes la valeur de
, il faut alors
regarder s’il y a exercice anticipé. Pour ce faire, on calcul
à l’aide de Black & Scholes la valeur de 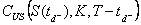 .
.
Remarque :
Sachant qu’il n’y a qu’un seul dividende,
le Call américain précédent est le même que
son homologue européen puisqu’il n’y pas de versement
de dividende pendant son exercice et que l’option américaine
n’est pas exercée de manière anticipée dans
ce cas. On aurait donc pu calculer ce Call par la méthode de Monte-Carlo
comme dans la partie précédente, mais il aurait alors fallu
implémenter un grand nombre de simulation, et ce pour chaque valeur
de 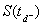 . C’est
pourquoi nous avons choisi d’utiliser ici la formule de Black &
Scholes.
. C’est
pourquoi nous avons choisi d’utiliser ici la formule de Black &
Scholes.
Pour chaque valeur de 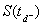 ,
on dispose de la valeur du Call qui permet de juger de l’exercice
anticipé. S’il y a exercice anticipé, on conserve
la valeur
,
on dispose de la valeur du Call qui permet de juger de l’exercice
anticipé. S’il y a exercice anticipé, on conserve
la valeur 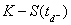 et on arrête la simulation pour cette valeur de
et on arrête la simulation pour cette valeur de 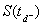 .
Sinon, on poursuit la simulation après avoir retranché le
dividende à la valeur
.
Sinon, on poursuit la simulation après avoir retranché le
dividende à la valeur 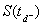 .
On obtiendra donc
.
On obtiendra donc 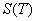 pour
lequel on calcul la valeur du Call qui est de
pour
lequel on calcul la valeur du Call qui est de 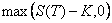 .
.
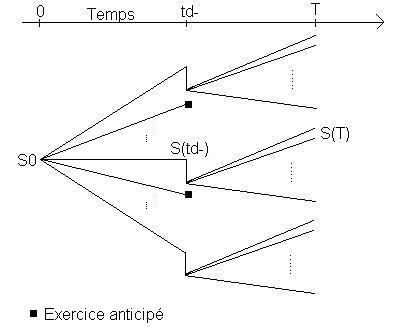
Pour chaque valeur de 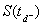 où il n’y a pas eu exercice, on obtient un grand nombre de
valeurs du Call en
où il n’y a pas eu exercice, on obtient un grand nombre de
valeurs du Call en  .
On effectue la moyenne de ces valeurs que l’on actualise en 0. De
même on calcul la moyenne des
.
On effectue la moyenne de ces valeurs que l’on actualise en 0. De
même on calcul la moyenne des 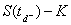 pour les Call qui ont été exercés, et on actualise
en 0. On effectue alors la moyenne de ces valeurs, pondérées
par les probabilités d’apparitions de l’exercice anticipé
et son complémentaire, on obtient la valeur du Call recherchée.
pour les Call qui ont été exercés, et on actualise
en 0. On effectue alors la moyenne de ces valeurs, pondérées
par les probabilités d’apparitions de l’exercice anticipé
et son complémentaire, on obtient la valeur du Call recherchée.