Proposition sur la recherche des polynômes générateurs :
Rappel :
Soit 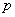 la caractéristique
de
la caractéristique
de 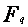 .
. 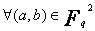 on a
on a 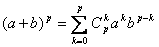 .
.
Comme 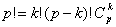 on en déduit
que pour
on en déduit
que pour  on a
on a 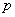 qui divise
qui divise 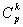 .
D’où
.
D’où 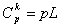 .
.
On a alors 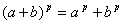 et ce
résultat peut s’étendre à
et ce
résultat peut s’étendre à  .
.
Reprenons :
On pose 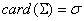 . On
a
. On
a 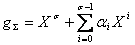 avec
avec 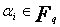 .
Donc
.
Donc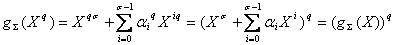 . D’où
. D’où
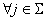 on a
on a 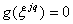 ce qui implique que
ce qui implique que  .
.
Or 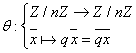 est un morphisme
additif. Donc
est un morphisme
additif. Donc 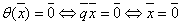 car
car
 .
.
On a alors 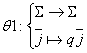 qui est une bijection. Donc
qui est une bijection. Donc  est stable par
est stable par  .
.
Réciproquement :
Soit  une partie
de
une partie
de 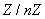 stable par multiplication
par
stable par multiplication
par 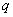 .
.  puisque
puisque  .
En effet, par récurrence sur
.
En effet, par récurrence sur  montrons que si
montrons que si 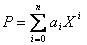 alors
alors 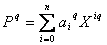 .
.
Pour  la propriété
est claire. Soit
la propriété
est claire. Soit 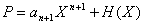 avec
avec 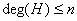 .
.
 avec
avec  pour
pour  car
alors
car
alors 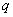 divise
divise 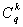 .
.
D’où 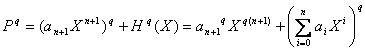 et par hypothèse de récurrence :
et par hypothèse de récurrence : 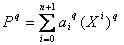 .
.
On a donc 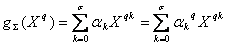 ce qui
implique que
ce qui
implique que  on a
on a  avec
avec 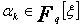 .
.
Or l’équation 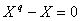 dans
dans 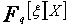 admet exactement
admet exactement
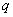 racines, en effet :
racines, en effet :
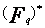 est un groupe
cyclique de cardinal
est un groupe
cyclique de cardinal 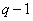 .
Donc
.
Donc 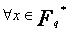 on
a
on
a 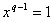 d’où
d’où
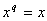 .
.
Donc les éléments de 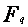 sont les racines de cette équation. D’où
sont les racines de cette équation. D’où 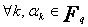 .
.
On a donc montré que 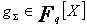 .
.
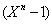 est un idéal
de
est un idéal
de  , on a alors que
, on a alors que
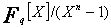 est une algèbre,
donc un
est une algèbre,
donc un 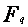 -espace vectoriel
de dimension
-espace vectoriel
de dimension  dont
dont 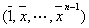 est une base. En effet :
est une base. En effet :
Soit , en utilisant la division euclidienne de 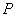 par
par 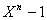 on a :
on a :
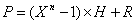 avec
avec  .
D’où :
.
D’où :
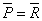 donc en
notant
donc en
notant 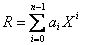 on
obtient
on
obtient 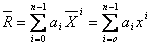 où
on confond
où
on confond 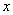 et
et 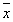 .
.
Ce qui prouve que la famille 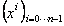 est génératrice de
est génératrice de 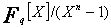 .
.
Reste à montrer que cette famille est également libre.
L'idéal de
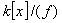 est engendré
par
est engendré
par 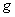 qui est unique :
qui est unique :
Soit 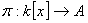 la projection
canonique. Si
la projection
canonique. Si 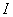 est un idéal de
est un idéal de 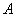 ,
,
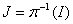 est un idéal
de l’anneau principal
est un idéal
de l’anneau principal 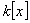 ,
et l’on sait que le polynôme
,
et l’on sait que le polynôme 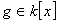 unitaire de plus bas degré de
unitaire de plus bas degré de 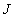 vérifie
vérifie 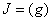 .
Comme
.
Comme 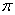 est surjective,
est surjective,
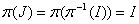 d’où
d’où
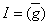 . De plus,
. De plus, 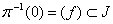 montre que
montre que 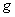 divise
divise  .
.
Montrons l’unicité :
Si  vérifie
vérifie
 ,
, 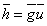 pour un polynôme convenable
pour un polynôme convenable 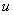 ,
donc il existe
,
donc il existe 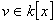 tel que
tel que 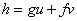 .
Comme
.
Comme 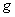 divise
divise  ,
,
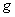 divisera
divisera 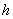 .
En recommençant de la même façon, on montre que
.
En recommençant de la même façon, on montre que 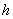 divise
divise 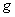 , de sorte que
les polynômes
, de sorte que
les polynômes 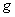 et
et 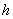 soient associés
et unitaires, donc égaux.
soient associés
et unitaires, donc égaux.
Montrons qu’un corps fini a un cardinal du type 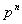 où
où 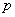 est un nombre
premier.
est un nombre
premier.
-> Soit 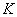 un
corps fini à
un
corps fini à  éléments, montrons que
éléments, montrons que 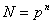 .
.
Rappel concernant la caractéristique :
En notant 1 le neutre de 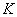 ,
on a
,
on a 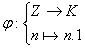 est un morphisme
d’anneaux. On a alors
est un morphisme
d’anneaux. On a alors 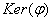 qui est un idéal de
qui est un idéal de 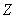 ,
d’où
,
d’où 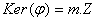 avec
avec
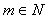 .
.
Si 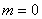 alors
alors 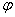 est un morphisme injectif, donc
est un morphisme injectif, donc 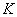 contient
contient 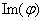 qui est
un anneau isomorphe à
qui est
un anneau isomorphe à 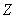 ,
ce qui signifie que
,
ce qui signifie que 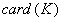 est infini, ce qui n’est pas le cas.
est infini, ce qui n’est pas le cas.
Remarque :
Si 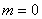 et
et 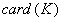 infini, alors
infini, alors 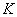 contient toute les fractions de
contient toute les fractions de 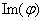 donc un corps isomorphe à
donc un corps isomorphe à 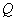 (ensemble des rationnels).
(ensemble des rationnels).
Donc on a 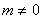 , ce
qui implique
, ce
qui implique 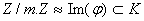 . Comme
. Comme
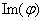 est un sous anneau
de
est un sous anneau
de 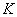 , qui est un
anneau intègre (car corps),
, qui est un
anneau intègre (car corps), 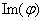 est lui aussi intègre donc de même pour
est lui aussi intègre donc de même pour 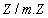 .
On en déduit que
.
On en déduit que 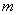 est un nombre premier que l’on notera
est un nombre premier que l’on notera 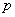 .
.
On a alors 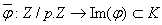 qui
est un isomorphisme, donc
qui
est un isomorphisme, donc 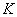 contient un sous corps
contient un sous corps 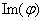 isomorphe à
isomorphe à 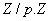 .
On dit que
.
On dit que 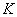 est
de caractéristique
est
de caractéristique 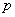 .
.
On a donc la situation suivante :
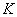 est un corps
fini à
est un corps
fini à  éléments,
éléments, 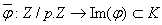 est un isomorphisme. En notant
est un isomorphisme. En notant 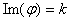 on a alors que
on a alors que 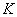 a une structure naturelle de
a une structure naturelle de 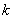 -espace
vectoriel.
-espace
vectoriel.
Si 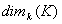 est infini alors
est infini alors
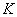 est infini, ce
qui est exclu. En effet, il contiendrait par exemple un système
générateur, donc un nombre infini d’éléments.
est infini, ce
qui est exclu. En effet, il contiendrait par exemple un système
générateur, donc un nombre infini d’éléments.
Donc 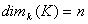 . Ce qui
signifie que
. Ce qui
signifie que 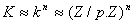 donc
donc
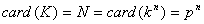 .
.
-> Réciproquement montrons qu’il existe un corps à
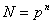 éléments
où
éléments
où 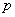 est premier.
est premier.
On admet qu’il existe un sur-corps 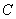 de
de 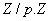 tel que
tel que 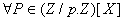 ,
,
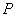 est scindé
sur
est scindé
sur 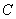 . On considère
alors
. On considère
alors 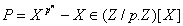 et
et 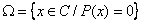 .
On a donc
.
On a donc 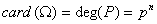 car toutes les racines de
car toutes les racines de 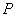 dans
dans 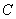 sont simples. En
effet,
sont simples. En
effet, 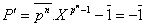 .
.
Si 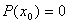 alors
alors 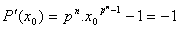 .
.