Pour des codes en bloc, si le taux d’erreurs en ligne est inférieur à la capacité de correction, la probabilité d’erreurs tend vers zéro lorsque la longueur du code augmente, à taux de transmission et capacité de correction constant. Il en découle que la construction de codes longs avec de bons paramètres, munis d’un algorithme de décodage dont la complexité croit aussi faiblement que possible avec la longueur, est un sujet fondamentale de recherche.
Le développement récent de la cryptographie montre que la recherche que nous venons de décrire s’applique généralement en codage. En effet les liens existant entre la cryptographie et la théorie des codes correcteurs se concrétisent en de nouveaux thèmes de recherche où l’utilisation des fonctions booléennes, de la théorie des corps finis et de certains algorithmes de codage, nécessite la compétence de spécialistes de la théorie des codes.

La recherche « pure » sur les codes correcteurs consiste en l’étude in abstracto des meilleurs codes possibles, sans se soucier, à ce stade de recherche, de l’existence d’un bon algorithme de décodage. On est ainsi amené à construire des codes ayant une structure algébrique de plus en plus complexe, en utilisant tous les outils de mathématiques discrète (algèbre des structures finies, combinatoire, géométrie finies). L’autre versant de la recherche se situe au niveau de la performance des codes, ce qui impose la recherche systématique de tous les paramètres d’un code donné ; l’existence et la complexité d’algorithmes de décodage sont alors un élément de l’étude. Ainsi le domaine de recherche, bien que centré sur l ‘étude d’un objet « mathématique », doit intégrer les outils modernes de l’informatique théorique, notamment l’algorithmique et le calcul formel.

Il est à noter que le champ d’application de ces techniques de décodage ne se cantonne pas à la résistance au bruit. Ils peuvent aussi servir à casser des schémas cryptographiques, ou être utilisés en bio-informatique par exemple.

Comment optimiser les codes :

On peut augmenter la distance minimale entre deux mots en rajoutant des bits. Mais rallonger le message accroît la durée et le coût des communications. Les concepteurs de codes correcteurs d’erreurs s’efforcent donc de trouver des algorithmes de codage performants, qui permettent de détecter et de corriger le maximum d’erreurs, tout en allongeant le moins possible les mots. De plus, les procédures de codage et de décodage doivent être suffisamment simple.

Deuxième théorème de Shannon :

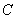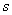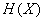Soit un canal de capacité transmettant symboles par unité de temps d’une source d’entropie dont le débit est un mot par unité de temps. C. Shannon a montré qu’il existe une méthode de codage qui garantit une transmission quasi parfaite (probabilité d’erreur arbitrairement faible) si : .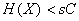
On peut interpréter ce résultat de la manière suivante : si un canal de transmission génère des erreurs de transmission, il est tout de même possible de trouver une manière de coder les messages émis en leur rajoutant suffisamment de redondance de sorte qu'on puisse retrouver le message émis sans erreur. Ce théorème ne dit pas comment construire un tel code. Le problème des spécialistes des codes correcteurs d'erreurs est de trouver des méthodes de codage qui se rapprochent autant que possible de la borne de Shannon. Une méthode qui parait prometteuse est celle des "turbocodes''.