Le Put américain.

Contrairement au Call Américain, le versement ou non d’un dividende n’assure en rien la possibilité d’exercice du Put. Il est donc nécessaire de vérifier pour tou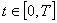t instant si exercer le Put est plus intéressant que de le conserver. On s’aperçoit donc qu’il faudrait théoriquement calculer la valeur du Put –et donc du sous-jacent– pour tout instant 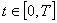, c'est-à-dire un nombre infini de fois. Il est donc évident que le modèle binomial va être préféré à la formule de Black & Scholes ; il existe bien une technique adaptant la formule de Black & Scholes à ce type d’option mais la valeur obtenue sera beaucoup moins précise que celle obtenue par le modèle binomial.

Explication du code utilisé pour le modèle binomial :

Le principe reste le même que celui utilisé pour les Call en présence de dividendes, cependant comme la présence ou non de ces dividendes ne permets pas de savoir a l’avance s’il va y avoir exercice ou non, nous avons pris le parti d’étudier un Put américain en l’absence de versement de dividendes. Nous obtenons donc un arbre possédant 101 valeurs finales en une seule étape. A partir de ces 101 valeurs finales nous obtenons 101 valeurs pour le Put américain en par la formule :

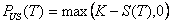
Nous pouvons à présent remonter l’arbre en utilisant la formule :

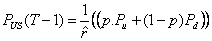
Cependant comme l’option est américaine il faut regarder si 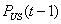est inférieur au prix d’exercice en 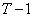. La véritable formule est donc :

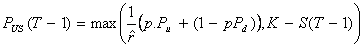
En utilisant cette algorithme on peut donc trouver aisément la valeur du Put américain à l’aide du modèle binomial.

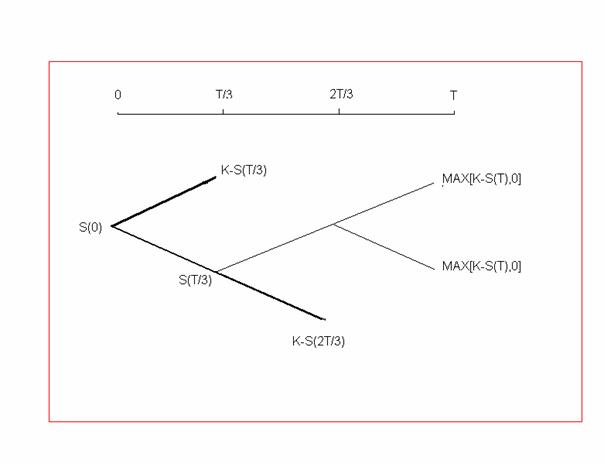
Nous allons donc maintenant calculer cette valeur à l’aide de la technique de Monte-Carlo. Comme il faudrait regarder la valeur du Put à chaque instant, on ne peut pas appliquer la technique de Monte-Carlo comme nous l’avons fait dans les études précédentes. Comme nous ne pouvons pas calculer le Put américain directement nous allons recourir à la formule de Geske et Johnson :

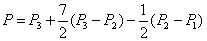
Cette formule –que nous ne démontrerons pas– permet d’exprimer un Put américain en fonction 3 Put aisément calculables. En effet 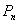n’est autre qu’un Put européen pouvant être exercé en .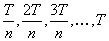

Calcul de :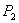

On simule un nombre de fois conséquente la valeur du sous-jacent en 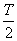, puis pour chaque 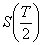simulé on vérifie si l’exercice anticipé est plus intéressant que de conserver le Put. Ceci ce fait grâce a la formule :

Exercice anticipé si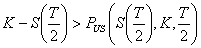

S’il y a exercice anticipé, alors on conserve la valeur 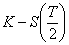et on arrête de simuler pour cette branche, sinon on simule la valeur de 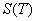à partir de 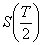et pour chaque valeur obtenue on regarde la valeur du Put. Ensuite on effectue la moyenne des Put où il y a exercice anticipé et la moyenne des Put exercés uniquement à l’échéance. On pondère chacune de ces valeurs respectivement par la probabilité d’exercice anticipé et par la probabilité d’exercice en fin de vie. On obtient ainsi la valeur de . 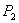On peut donc maintenant calculer la valeur de .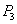

Calcul de :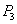

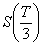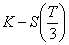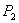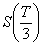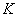On simule la valeur de puis on compare la valeur avec la valeur d’un Put de type de sous-jacent , de prix d’exercice et de maturité .
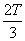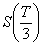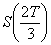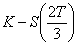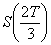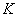Les valeurs de pour lesquelles l’exercice anticipé n’est pas intéressant nous permettent d’obtenir . On compare alors la valeur avec la valeur d’un Put européen de sous-jacent , de prix d’exercice et de maturité .
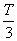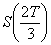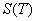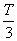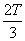Les valeurs de pour lesquelles l’exercice anticipé n’est pas intéressant nous permettent d’obtenir . On en déduit pour ces valeurs la valeur du Put à maturité. Il ne reste plus qu’à sommer la moyenne des prix si exercice en , plus la moyenne des prix si exercice en , plus la moyenne des Put à échéances pondérés de leur probabilité d’apparition respective.
On obtient ainsi à l’aide la formule de Monte-Carlo la valeur du Put .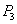

Détermination de la valeur du Put :

On sait calculer facilemen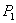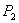t , et 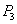. On peut donc déterminer la valeur du Put américain à l’aide de la formule de Geske & Johnson :

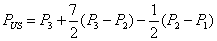
Conclusion :

Contrairement au cas des options européennes, l'utilisation de la technique de Monte-Carlo afin de simuler des options américaines est beaucoup moins facile et moins instinctive. En effet une option américaine nécessite de vérifier l'intérêt d'exercer l'option à plusieurs instant, voire à tout instant. L'utilisation de la technique de Monte-Carlo va donc nécessiter de calculer de nombreuses options de types européenne alors que le modèle binomial ne nécessite que la construction de l'arbre de et de l'arbre du Call. Le calcul par le modèle binomial d'une option américaine ne nécessitera donc pas beaucoup plus de calcul que pour le cas d'une option européenne. La technique de Monte-Carlo est donc plus complexe et ne sera pas plus précise que le modèle binomial. Son intérêt reste donc très limité.