Les informations qui circulent sur les lignes téléphoniques sont regroupées en blocs de 15 octets dont le dernier bit de chaque octet est un bit de parité. On ajoute alors à ce bloc un 16-ième octet de CRC (Contrôle de Redondance Cyclique) et un dernier dit de validation.
L’octet de validation est égal à 0 , il permet de détecter les importantes pertes d’informations sur la ligne : si un ou plusieurs bits de cet octet sont modifiés, on demande alors le renvoi du paquet ; de même s’il on détecte une erreur multiple en analysant les bits de parité de chaque bloc.

Voyons l’octet de CRC. Le message est formé de 120 bits noté 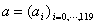que l’on identifiera au polynôme 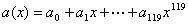. On utilise alors un code cyclique de longueur 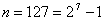et le polynôme générateur 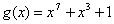. On a bien qui est le polynôme minimal sur d’une racine 127-ième primitive de l’unité.

Codage du message :

-> On effectue la division euclidienne de 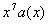par : .
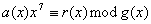-> Les coefficients de 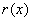sont alors les 7 premiers bits de l’octet CRC.
-> Le dernier bit est un bit de parité portant sur les 7 premiers.
Ainsi on envoie le message 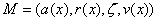constitué du message effectif, du reste, du bit de parité sur le CRC et de la validation.

Décodage du message :

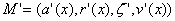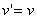On reçoit le message , et on suppose et que 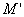ne contient qu’une seule erreur, auquel cas on n’a pas a traiter la correction. Si tous les bits de parité de 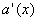sont justes ainsi que 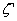on considère que 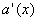est le message envoyé.
Supposons donc que 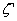soit faux. L’erreur est dans 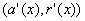et on a 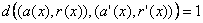. Il existe donc un entier 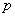tel que 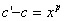. En prenant les classes modulo , on obtient 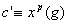. Le lemme suivant permet de savoir exactement où l’erreur s’est produite en retrouvant .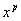

Lemme :

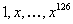sont des classes distinctes de 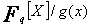. C’est à dire 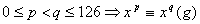. Si 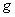divise 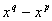alors 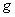divise 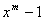où 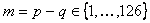. L’un des zéros de 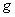est une racine 127-ième primitive de l’unité, notée 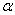, et on a 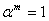, ce qui est absurde.