Je vous présente ici 2 exemples triviaux, puis un exemple de construction
d'un polynôme générateur de code cyclique.
Ce code, qui consite à répèter  fois chaque bits, a une distance minimale égale à
fois chaque bits, a une distance minimale égale à  .
Il permet de corriger un nombre inférieur à
.
Il permet de corriger un nombre inférieur à  erreurs
de transmission par un simple algorithme majoritaire. Mais la dilution
extrême du message entraîne un taux d’information de
erreurs
de transmission par un simple algorithme majoritaire. Mais la dilution
extrême du message entraîne un taux d’information de
 . (il faut prendre
. (il faut prendre
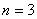 pour corriger au
moins une erreur).
pour corriger au
moins une erreur).
La forme la plus simple de détection d’erreur est l’adjonction
aux mots du message d’un bit de parité. Soit, par exemple,
un message comportant 7 données binaires. On compte le nombre de
bits égaux à 1. Si ce nombre est pair, le bit de parité
rajouté vaudra 0, si ce nombre est impair le bit de parité
vaudra 1. De cette façon le message émis de longueur 8 aura
toujours un nombre de bits égaux à 1 qui sera pair (parité
égale à 0). Si le message reçu à une parité
égale à 0, on considérera que le message a été
correctement transmis. Mais il peut y avoir deux erreurs de transmission,
ce bit de parité ne permettra pas de détecter cette forme
d’erreur. Si la parité du message est égale à
1, on sait qu’il y a certainement une erreur de transmission. Mais
il n’est pas possible de retrouver la donnée erronée.
Voici un exemple d'application du code par bits de parité ; ici
en passant les "mots" sous forme de matrices, on obtient un
code qui est 1-correcteur. On a ici un mot de 4 bits que l’on code
en une matrice carrée en haut à gauche ; puis on rajoute
une ligne et une colonne dont les coefficient sont égaux à
la somme des bits de la ligne ou de la colonne. Lorsque l’on reçoit
un message muni d’une erreur, on retrouve sa position par l’intersection
ligne colonne et on le décode facilement puisque nous sommes en
binaire.

Construction d'un polynôme générateur :
Travaillons avec  .
On dispose de 2 choix de partie
.
On dispose de 2 choix de partie  de
de  :
:  et
et 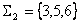 .
.
Travaillons avec  ,
on a :
,
on a :
 où
où  est une racine 7-ième primitive de l'unité. On obtient
est une racine 7-ième primitive de l'unité. On obtient  .
.
Or 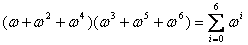
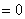 car on travaille dans
car on travaille dans  .
.
D 'où  ou
ou
 .
.
Si  alors
alors  car
car  .
.
De même dans l'autre cas. On a donc le choix entre les 2 polynômes
générateurs suivant :  et
et  .
.
De plus, on obtient les mêmes résultats en travaillant avec
 , ce qui prouve
qu'il n'existe que 2 polynômes générateur du code
, ce qui prouve
qu'il n'existe que 2 polynômes générateur du code
 .
.